‘Walk this Way’: FSU researchers’ model explains how ants create trails to multiple food sources

It’s a common sight — ants marching in an orderly line over and around obstacles from their nest to a food source, guided by scent trails left by scouts marking the find. But what happens when those scouts find a comestible motherlode?
A team of Florida State University researchers led by Assistant Professor of Mathematics Bhargav Karamched has discovered that in a foraging ant’s search for food, it will leave pheromone trails connecting its colony to multiple food sources when they’re available, successfully creating the first model that explains the phenomenon of trail formation to multiple food sources.
Karamched, who also serves as faculty in FSU’s Institute of Molecular Biophysics, and music arts administration graduate student Sean Hartman, published “Walk This Way: Modeling Foraging Ant Dynamics in Multiple Food Source Environments” in the Journal of Mathematical Biology in September.
“The power of mathematics is that we can devise models that reproduce experimentally observed data and make concrete predictions about what will happen next,” Karamched said. “In this case, we uncovered something that hasn’t been described well by other models: if an ant has access to multiple food sources from its nest, it will initially make multiple trails to each of the sources.”
Karamched uses modeling, mathematical analysis and computer simulations to understand and solve problems in neuroscience and cell biology. Hartman, who earned dual bachelor’s degrees from FSU’s Department of Mathematics and College of Music in May 2023 and expects to complete his graduate studies this spring, approached Karamched about assisting with a Directed Individual Study (DIS). DIS allows students in FSU’s Honors Program to work one-on-one with faculty mentors in an open-ended, hands-on research experience and would allow Hartman to be more involved with mathematical modeling.

“I wanted to pursue research in mathematics, as I’ve had a lifelong interest in the subject, but never had the opportunity to take part in math-based research until now,” Hartman said. “I was intrigued by ant trail research that Dr. Karamched shared with me and became interested in pursuing further research on it and creating models based on this previous work.”
Foraging for resources is an essential process for the daily life of an ant colony, and ants will self-organize using chemical pheromones. Once an ant detects a food source, it secretes a chemical trail to lead other ants to the source. Using computational simulations of ants searching for food, stochastic modeling and a system of partial-differential equations, the researchers also observed that over time, ants will selectively travel to the food source that is the shortest distance from its nest in an environment with multiple sources.
“For this research, we divided the ants into two subpopulations: foragers and returners,” Karamched said. “These subpopulations behave differently, as foragers tend to wander around in search of food while returners always return directly to the nest after finding food, making their motion less stochastic or random. This allows us to predict with 100 percent certainty what they’re doing or where they would go.”
The team, including collaborator Shawn Ryan, associate professor in the Department of Mathematics and Statistics at Cleveland State University, considered the concentration of chemical pheromones that the ants secreted, signaling to other ants where food is. The probability of their models was based on the dynamics of these pheromones. The returning ants would secrete less pheromones depending on how close the food source was to the nest. More pheromones created a stronger scent for the ants to follow, a critical factor when the food source is located far from the nest.
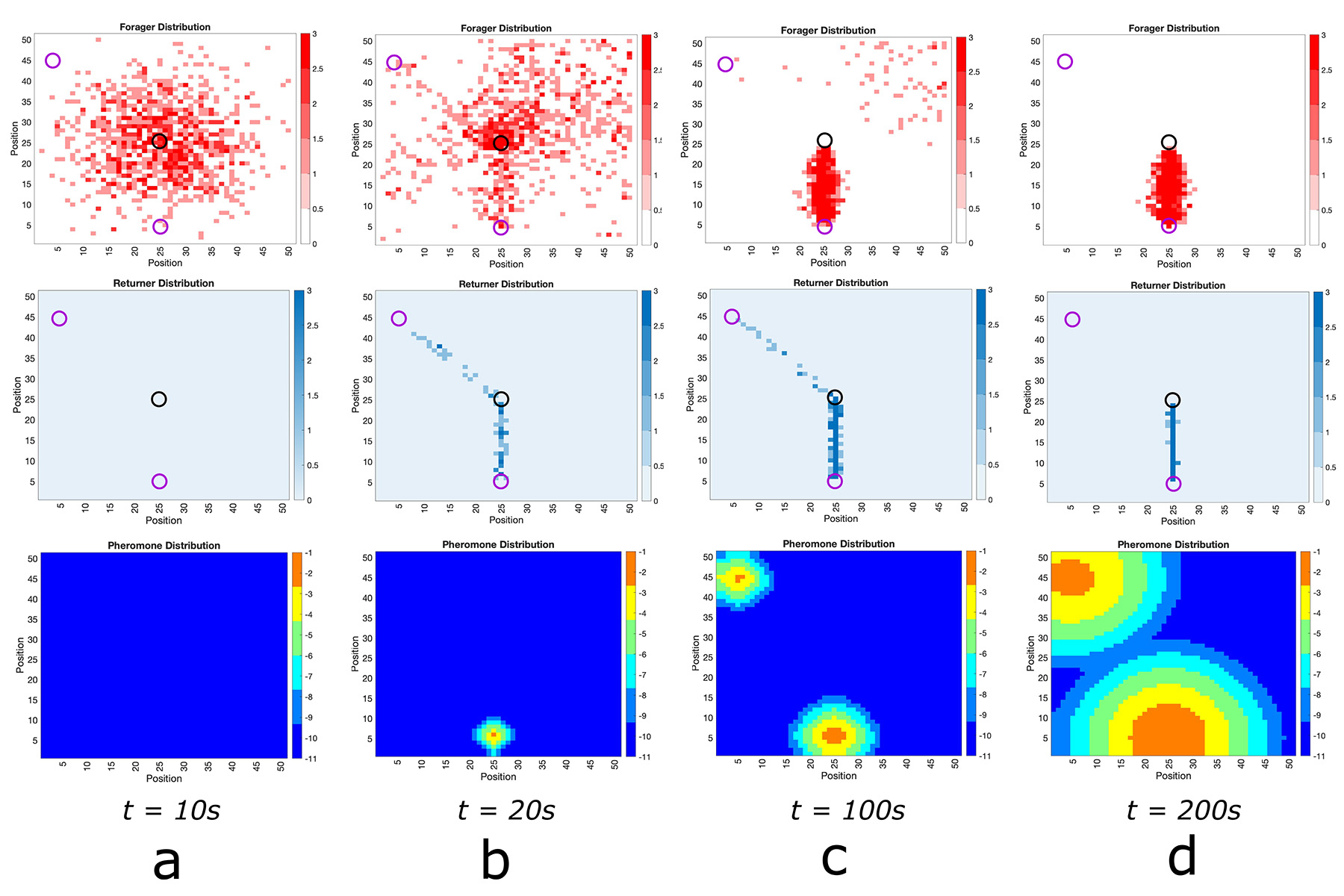
“Once my code was fully tested and accurate, multiple trail formations became distinct and were easily understandable,” Hartman said. “It was so cool to see how equidistant food sources could maintain multiple food trails as an equilibrium. If one food source was just slightly closer to the ants’ nest, the ants would eventually form one singular trail to the closest source. It was at this moment that it felt all our hard work finally paid off.”
The model in this paper was designed to be simple and applicable to other organisms and biological systems that use pheromones as a form of communication, including bacteria, slime molds, other insects, fish, and even some reptiles and mammals.
“The framework for analyzing this collective behavior resides in the fundamental pheromone concentration gradient, then working from there,” Karamched said. “From a microbial level to complex organisms, using this chemical signaling to communicate allows certain organisms to coordinate activity on huge spatial scales, which is fascinating.”
To learn more about Karamched’s research and the FSU Department of Mathematics, visit math.fsu.edu.
